Why did we write Cinderella? Aren't there enough programs that are suitable for doing mathematics, and in particular for producing mathematical graphics? Well, there are many programs, but Cinderella is special in many respects.
We want to point out the major features of this software. Cinderella ...
The application areas of Cinderella reach from pure Euclidean (and non-euclidean) geometry, via physics (optics, for example) to computational kinematics and CAD. The following sample applications present potential scenarios which you can benefit by using Cinderella.
Assume you are writing a scientific publication for which you need one or more figures. When the drawings are a bit involved it is usually almost impossible to make a perfect one on the first attempt.

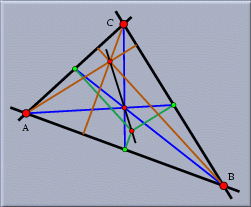
|
| The Euler Line of a triangle |
Either you will have many elements in almost the same place, or some parts of the figure will not fit onto the page.
With Cinderella you start by making a computer sketch of a construction. This sketch might not look like what you expect the final drawing, but it provides all relations that are decisive for the construction. Later you pick the base elements and move them around until the picture satisfies all your esthetic requirements. During the "move phase" you will always have a valid instance of your geometric construction. Finally you use Cinderella's Appearance Editor to adjust the color and size of each geometric element.
Sometimes it happens that you want to get a feeling for some geometric situation. Either you have read something interesting in a geometry book or you have a new idea yourself.
You do the construction with Cinderella and start to play with it. Through geometric exploration you gain new insights and often hidden properties are revealed. Cinderella's mathematically consistent implementation ensures that no strange effects occur that do not come genuinely from the configuration.
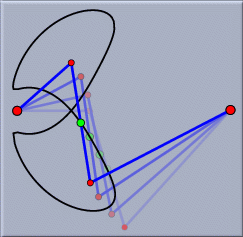
|
| Dynamics of a three bar linkage |
When you want to communicate your research to other colleagues you create an interactive web page and make it available on the internet. Then your colleagues have instant access to the configuration and can interact with it locally in their Java-enabled web browser.
Another interesting application is the generation of interactive student exercises. Imagine that you want to teach students how to construct the circumcenter of a triangle using only ruler and compass. First you do the construction yourself. Then you create an interactive exercise by marking the "input elements", providing exercise texts, marking "intermediate construction steps" and the "final result". Cinderella generates an interactive Web page that presents the input elements (perhaps the triangle from which the students should start) together with all the construction tools for doing ruler and compass constructions.
The students can solve the exercises on their own computer and arrive at a solution completely by themselves or by following hints you provided. No matter which construction a student used to solve the problem, Cinderella's integrated automatic theorem checking facilities can decide whether it is correct or not. The student's creativity for finding a solution is not restricted by the program.
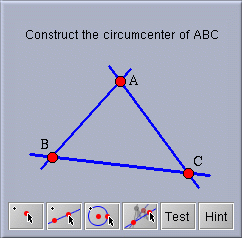
|
| An exercise for students |
Several major design goals lead us in the development of Cinderella. We want to mention the three most important ones to give you an impression of the overall architecture of the program.
General approaches: Cinderella is designed to cover a broad range of geometric disciplines. The program provides "native support" for Euclidean Geometry, hyperbolic geometry, elliptic geometry and projective geometry.
This means that you do not have to simulate hyperbolic geometry by making complicated Euclidean constructions. You can use the "hyperbolic mode" of Cinderella and the constructions will behave like elements of the hyperbolic plane.
Cinderella achieves this by implementing very general mathematical approaches to geometry that form a common background for all of the above areas. Much of the mathematics behind Cinderella makes use of the great, and unfortunately almost forgotten, geometric achievements of the geometers of the nineteenth century. To mention a few of them: Monge and Poncelet who "invented" projective geometry; Plücker, Grassmann, Cayley and Möbius who developed a beautiful algebraic language to deal with projective geometry; Gauss, Bolyai and Lobachevsky who "discovered" what is today called hyperbolic geometry; and finally Klein, Cayley and Poincaré who managed to get a unified description of Euclidean and non-euclidean geometries in terms of projective geometry and complex numbers. For an excelently written and exciting introduction to the historical development of geometry in the nineteenth century we recommend the book of Yaglom [Yag]. Also the historical book [Kl1] written by Felix Klein himself is a very interesting introduction into this topic.
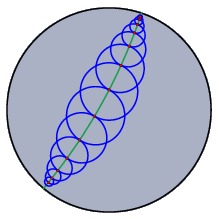
|
| Hyperbolic circles of equal size |
Projective geometry forms the background for the incidence geometry part of Cinderella and Cayley-Klein geometries form the backbone for the metric part of Cinderella.
Mathematical consistency: To say it in a metaphor: "The geometric constructions done with Cinderella should behave as if they lived in a reasonable geometric universe. In this universe, no unnatural things should happen".

|
| Offset curve of a parabola - a challenge for most CAD systems |
Other systems for dynamic geometry suffer from mathematical inconsistencies. You do a construction, drag around the base elements and suddenly one part of the construction jumps from one place to another. This is unfortunately a usual scenario in other systems for dynamic geometry or of parametric CAD.
Cinderella completely resolves this problem by using a new theory. It makes use of features from complex analysis and merges them with the "old geometry" mentioned above.
Based on this theory it was possible to equip Cinderella with an automatic theorem checker that governs most of the internal decisions Cinderella makes. This theorem checker is also used for automatic feedback operations in student exercises. Another benefit of this approach is that you have a generic tool to construct correct and complete geometric loci, which are real branches of algebraic curves.
Modular design: Cinderella is designed to be as modular as possible. This architecture makes Cinderella well prepared for further extensions in many directions.
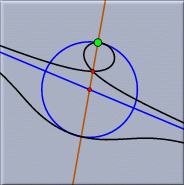
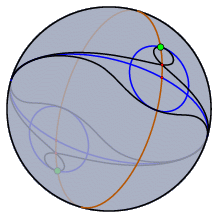
| 
|
| Conchoidal curve in a Euclidean | and in a spherical view. |
Even the present release benefits from the modular approach. For instance, it is possible to view the same geometric constructions simultaneously in many geometric contexts. A construction in hyperbolic geometry can be simultaneously shown, and manipulated, in the "Poincaré Model" of hyperbolic geometry and in the "Beltrami-Klein Model". The simultaneous use of different views helps to gain a deeper understanding of a configuration. For example, the "behavior at infinity" of a configuration becomes immediately visible in a spherical view.
Normally you would, and should, not care about the programming language and other technical details of software you just want to use. Nevertheless, we want to tell you about the computer science background of Cinderella.
Cinderella was written in Java, the platform independent programming language developed by Sun Microsystems. This means that the software can be run on any computer, irrespective of its operating system, provided that there is a thing called the "Java Virtual Machine" (JVM) for this system. These Java Virtual Machines are available from Sun Microsystems for Windows 95/98/NT and Solaris, and there exist ports for Linux, OS/2, MacOS, BeOS, AIX, HP-UX and many more. In fact, you probably already have a JVM installed on your computer, since Netscape Navigator and Microsoft Internet Explorer have a built-in JVM. This, in turn, means that you can run Java programs inside a web browser. These programs are known as "Applets".
We do not want to explain Java in full detail here, instead we recommend the official Java home page at http://www.javasoft.com as a starting point for further reading. However, we do want to tell you about some of the consequences of choosing Java for Cinderella.
It is a fact that, although Microsoft Windows is the dominating operating system today, many mathematics departments have a variety of Unix workstations. Even within the same working group you can find a mixture of different systems. Java enables everybody, regardless of the choice of platform, to use Cinderella in the same way. It is even possible to install and use the same code on all of your computers. For us, we could use our favorite operating system (Linux) for development, and at the same time we were sure to reach the largest possible audience.
Second, the fact that you can run Java software inside web browsers has been used for the web export functionality of Cinderella. This means that you can publish constructions easily, spice up your personal home page with animations, or assign construction homework to your students. Our license agreement gives you great freedom in redistributing the necessary parts of Cinderella, but please obey the few restrictions that come with it.
Java is an interpreted language, as opposed to compiled languages like C or C++, which are the usual languages used for most software. Interpreted languages have some technical advantages, but they suffer from an additional translation step which slows the program down. Java (or the virtual machine) has been tuned a lot for performance, and the performance gap is not as large as it was when our project started. Still we had to do a lot of optimization by hand to create acceptable speed, and the "interactive feeling", of Cinderella.
Sometimes you'll notice a short delay when you move a point. Do not blame your computer, Java or Cinderella. These delays are caused by extremely complex calculations which are necessary to get the correct result or the correct screen representation after a movement. The generation of correct loci is one reason for that; many intersections involving conics are the other. We tried our best to speed up these calculations, but there is a (mathematical) limit where we do not want to sacrifice accuracy for speed.
Finally we want to mention the tools that helped us in creating Cinderella and this documentation. First there is XEmacs, a powerful, extensible text editor, which is based on GNU Emacs, which in turn is a version of the original Emacs written by Richard Stallman in the seventies at MIT. It is definitely the best editor available, and we used it to write the whole program and all of the documentation.
The program itself was developed with the help of the Java Development Kit of Javasoft, a division of Sun Microsystems, in particular with the Linux port of it (see http://java.blackdown.org for more information on the Java-Linux porting project). Linux is a free, unix-like operating system originating from the work of Linus Torvalds, and is now continually improved by the effort of several hundred developers all around the world.
The parsing engine (used for loading saved constructions) was constructed with the help of ANTLR 2.5.0, a public-domain Java/C++ parser generator, written by Terence Parr of the MageLang institute.
Post-optimization and compression of the code was done with Jax from alphaworks, the research division of IBM. We want to thank the Jax team, in particular Frank Tip, for their help and IBM for the permission to use Jax commercially.
The Concurrent Versions System (CVS) by Cyclic Software did most of the version merging (and saved us from a lot of headaches). It is free software, too.
Thanks to the "browser war" between Microsoft and Netscape, the licensing terms for redistributing Netscape Navigator allow us to ship a Java-1.1 compatible browser with Cinderella.
The documentation of Cinderella, both the printed manual and the online version, were written with XEmacs in HTML. We used the same files for the printed version and the screen representation. The design of the web pages uses Cascading Style Sheets (CSS); the hardcopy was created using a whacked version of html2ps by Jan Karrman.
The icons and images used in Cinderella were designed by ourselves with The GIMP (GNU Image Manipulation Program), written by Peter Mattis and Spencer Kimball. In our view it is one of the most impressive freely distributed pieces of software. The additional figures in the documentation were created with Cinderella, of course, and Povray, a free 3D raytracing software, and some PostScript hacking.
Two people deserve special mention: James Gosling, the creator of the Java programming language, and Jamie Zawinski, responsible for the first Unix versions of Netscape Navigator. They are both connected to XEmacs in a special way: James Gosling did the first C-implementation of Emacs, known as GOSMACS, and Jamie Zawinski was the person responsible for XEmacs versions 19.0 to 19.10, which was at that time a collaborative work of Lucid (now out of business) and Sun Microsystems (sic!).