How should a system for doing dynamic geometry behave when a user interacts with it? In a sense the requirements are similar to the requirements for other programs:
Unfortunately, under these requirements dynamic geometry turns out to be a difficult subject. There are two main reasons for this:
Our usual "everyday geometry" is full of special cases. Two lines can intersect or they can be parallel. Two circles can intersect in one or two points or not at all. So, even for static constructions it is sometimes difficult to figure out what a correct and reasonable result for such a special case is. For instance, what is the angular bisector of two parallel lines? Is it undefined? Can it be any line parallel to the lines? Should it be a line that is equidistant to the two lines?
We could try to exclude all the special cases and not consider them at all. However, on the one hand this would mean excluding non-esoteric cases such as parallel lines. On the other hand, when we allow points to be moved in a construction it happens all the time that dependent elements are forced into special cases. Observe that this is still a static problem!
These kinds of static problems were studied for a long time. The great geometers of the nineteenth century were aware of them, and it is due to their effort that most of them could be solved. The key to a solution is to gradually extend Euclidean Geometry to a larger setup. First the usual plane is extended by elements at infinity, leading to Projective Geometry. Then the underlying algebraic structure is extended to cover complex numbers. This essentially removes all special cases from geometry.
It was an exciting development of mathematics how these approaches finally, around 1870, lead to a completely consistent system. This system explains the effects of euclidean geometry as well as the effects of non-euclidean, for instance hyperbolic, geometry. Today it is called "Cayley-Klein geometry" in memory of two of its main contributers.
The mathematical background and the implementation of Cinderella rely on this general setup. In this way Cinderella can deal with all special cases, and as an additional benefit is able to do non-euclidean geometry as well as Euclidean Geometry. It is an amazing fact that by using these general principles the program does not become more complicated. On the contrary: The exclusion of special cases allows a much simpler "straightforward" program structure.
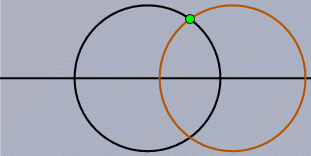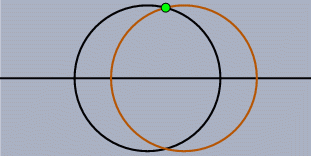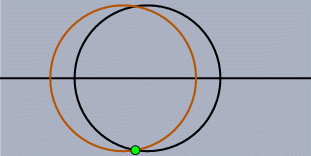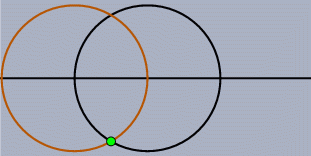
For systems of dynamic geometry there is a second class of problems, which are in a sense more subtle than the static problems. Unfortunately they lead to even more drastic effects. Assume you have done a construction that involves points, lines and circles, and in particular the intersection of two circles (or of a circle and a line). While you move the mouse the program has to decide, for every position, where the dependent elements are. However, there is a problem. Two circles do not have only one intersection - they have two, and we get both from our calculations. How should the system decide which of them is the one you "want"? When you construct the intersection the answer to this question is easy: "Take the point that is closest to the current mouse position." But when you start to move the problem there is no immediate answer.
What would be the most desirable is a continuous behavior of the program in the following sense:
"If you make a very small move with a free point, then the elements that depend on it should also move only a little bit."
At first sight it is not clear whether this requirement is satisfiable in general. Turn on your favorite system for doing dynamic geometry or parametric CAD and make the following experiment: Draw a horizontal line and construct two circles of equal radius whose centers can only slide along the line. Move them to a position where they intersect and construct the upper point of intersection of the two circles. Now move one circle so that its center passes through the center of the other circle. Most probably you will see that the point of intersection suddenly jumps from the upper intersection to the lower one; it happened in all the systems we tried so far. Such a behavior counters our requirement of continuity: You make a small move, and a dependent point suddenly jumps.

|
| This should not happen |
At first a single jumping point seems to be a kind of curiosity that is tolerable. But what happens if large parts of a construction depend on this jumping point? Then these parts of the construction will jump too, without prior warning. Most systems for dynamic geometry use heuristics based on orientation decisions that help to get rid of some of these jump situations. But still in every system many cases remain unresolved. Actually, there is a proof that no heuristic based on orientations only will be able to resolve all of these dynamic problems [KRG]. In an article on dynamic geometry [Lab] Jean-Marie Laborde, the main designer of Cabri Géomètre, states this dilemma in the following way:
"I think we need a real mathematical treatment of all consequences of stretching geometry in some way to a wider (dynamic) system. This system cannot be the projective one if we want to maximize the way the environment takes into account the special characteristics of non-static objects which are at the core of dynamic geometry."
Cinderella is the first program that is based on a theory which is capable of preventing dependent elements from jumping. This theory is also based on the use of complex numbers, which were used to solve the problems of static geometry.
The use of this theory has many benefits. For instance, it is the basis of the generation of correct loci. Consider the "three-bar-linkage" example of the second tutorial. The generation of the locus is based on the correct calculation of the points of intersection of two circles while a free point moves. In a other systems for dynamic geometry you will probably only get half of the eight-curve. The methods for automatic theorem proving, which are used internally throughout Cinderella, are based on this theory, too.
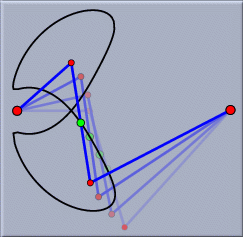
|
| The "three-bar locus" revisited |
The following pages should give you an impression of the different mathematical methods and theories that form the basis of the implementation of Cinderella.
The first and perhaps most important step for a consistent geometric setup is to extend the usual Euclidean plane to contain elements at infinity. You have surely heard the phrase "parallel lines meet at infinity", and you might believe it when looking from a bridge along a very long and straight railroad track. This phrase is the key to "Projective Geometry." The extension of geometry by infinite elements removes a lot of special cases from usual Euclidean Geometry.
Projective Geometry has a very long tradition. Its historical origin traces back to the study of perspective undertaken by famous painters such as Albrecht Dürer and Leonardo da Vinci. Its mathematical origin is the work of Gaspard Monge, a French geometer, who developed, around 1795, a method called descriptive geometry for representing spatial configurations by planar perspective drawings. Monge observed that non-trivial facts about planar geometric configurations could be derived by considering these configurations as projections of configurations in space. The study of parallels in these projections was most elegantly done by extending the plane by elements at infinity.
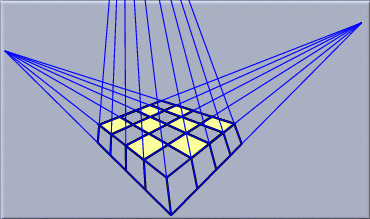
|
| In perspective drawings parallels actually meet |
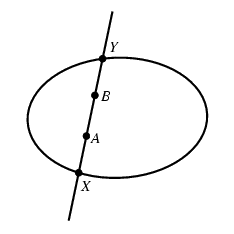
The projective plane consists of the points of the usual, Euclidean, plane together with one additional "infinite" point for every possible direction. The lines of the projective plane are the Euclidean lines together with one special "line at infinity." All infinite points lie on the line at infinity. The following, nicely symmetric, relations between points and lines hold:
The first person who formalized these rules, this was around 1822, was Victor Poncelet, a student of Monge, who today can be called the "father of Projective Geometry." In Projective Geometry there is no need to consider parallels as something special. They still have a point of intersection, it just happens to lie at infinity. For a readable introduction to Projective Geometry we refer to the books of H. S. M. Coxeter on that topic [Cox1, Cox2].
On a computer we unfortunately do not have geometric objects as primitive data types. A point or a line has to be represented by numbers: the coordinates. Usually a point in the plane is described by its (x,y)-coordinates. A line may be given by the three parameters (a,b,c) of its defining equation ax + by + c = 0. However, when we want to do Projective Geometry this turns out to be impractical. Each point coordinate (x,y) represents a finite point and there is no representation for the points at infinity. The correct solution to this problem became gradually clear in the first half of the nineteenth century. It started with Möbius' barycentric coordinates, via the refined setup of homogeneous coordinates given by Plücker, and finally lead to Grassmann's setup of multilinear algebra.
The way out of the dilemma is as follows. For every point we use three instead of two coordinates, introducing a third dimension. Consider the following scenario: The plane is embedded parallel to the x,y-plane of three-space at a height of z = 1, so it does not pass through the spatial origin.
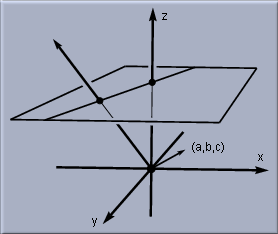
|
| Embedding the plane in space |
Every point (x,y) is represented by its three-dimensional coordinates (x,y,1). These coordinates are the homogeneous coordinates of the point. What happens with the rest of the points in the three dimensional space? Almost all of them will be interpreted as points in the original plane: we identify all three dimensional points that differ by a non-zero multiple. For instance, (4,6,2) and (2,3,1) describe the same point. In general, a point with spatial coordinates (x,y,z) is identified with the point (x/z,y/z,1) of the original plane. This process is called de-homogenization. In a way every point of the original plane corresponds to the line spanned by this point and the origin in three-space.
However, there are points in three-space that do not correspond to points in the original plane. The points of the form (x,y,0) cannot be de-homogenized in the above way, since then we would have to divide by zero. These points correspond precisely to the "points at infinity" of Projective Geometry. To see this, we study the behavior of a point that gradually moves to infinity in the original plane.
Assume that the moving point has coordinates (r,r). When r becomes larger and larger this point gradually approaches a point at infinity in the 45° direction. Looking at its homogeneous coordinates we see that they have the form (r,r,1)~(1,1,1/r). When r increases, the contribution of the first two coordinates dominate the last coordinate. In the limit case where r equals "infinity" the homogeneous coordinates are given by (1,1,0), an infinite point. You can also try to imagine the line through this point and the three dimensional origin. When the point approaches infinity this line becomes more and more horizontal, until, in the limit case, it is entirely contained in the x,y-plane.
A similar representation can be given for lines. For the line ax + by + c = 0 we take the parameters (a,b,c) as the homogeneous coordinates of the line. As in the case of points we identify non-zero multiples of such coordinates, since they do not alter the solution space of the corresponding equation. There is one set of parameters (0,0,1) that does not correspond to a finite line. This is the line at infinity. The vector (a,b,c) of a line is orthogonal to the plane spanned by the corresponding line and the origin of three-space. In particular the vector (0,0,1) is orthogonal to the (x,y)-plane, the "line at infinity."
In fact, the algebraic notion of homogeneous coordinates provides a complete symmetry between points and lines. Each point or line is represented by three homogeneous coordinates. A point (x,y,z) lies on a line (a,b,c) if and only if the scalar product ax + by + cy is zero - this is nothing but rewriting the equation of the line. Geometrically this means that the two corresponding vectors are orthogonal in three-space.
Not only geometry was extended throughout the centuries. A similar process happened to numbers, too. Probably the first numerical concept considered by mankind were the integers: 1, 2, 3, .... Starting from there it was reasonable to gradually extend the system of integers to more powerful concepts. The negative numbers, the rational numbers and the real numbers had to be invented to get a useful and self-contained system. The observation that there must be numbers that cannot be represented as fractions of two integers is of geometric nature and dates back to approximately 600 BC. It was seen by the Pythagoreans that there is no rational number measuring the length of a diagonal of a quadrangle with sides of length one. Applying Pythagoras' Theorem this task is equivalent to finding a number x with x² = 2. This discovery lead to a deep crisis in the foundations of ancient geometry.
However, the story of extending the number system does not stop at that point. One of the extensions, with perhaps the most drastic consequences, was the introduction of complex numbers. It was Geronimo Cardano in his Ars Magna that appeared in 1545 who was first to explicitly propose such an extension of the reals. He was lead to his conclusions by the study of solutions of polynomials of degree three. Based on the work of other contemporary mathematicians he discovered that a complete systematic representation of these solutions can only be given with the help of hitherto unknown values.
A complex number is a number of the form a + i·b where i satisfies the equation i² = -1, and a and b are real numbers. Clearly the number i cannot be any real number since the square of a real number can never be negative. The system of complex numbers is, just like the real numbers, closed under addition and multiplication. In other words the sum and the product of two complex numbers can again be written in the form a + i·b for suitable parameters a and b. However, unlike the real numbers the system of complex numbers is also closed under the operation of finding solutions of polynomials. For instance, consider the polynomial:
| x² - 6x + 13 = 0. |
As you can easily check it has no real solutions, but the complex numbers 3 + 2i and 3 - 2i do solve this equation. In fact, the following beautiful result is true: Every polynomial with arbitrary real or complex coefficients has all its solutions again in the field of complex numbers.
In a sense the discovery of complex numbers is the starting point for most modern mathematics. Many mathematical theories find their broadest, most elegant and most economic setting when they are formulated over the complex numbers. This happens also to geometry. Consider the situation of two circles. Depending on their position they can have two, one, or no points of intersection.
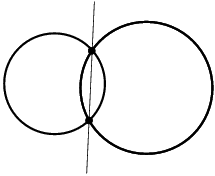
| 
|
| Circles can intersect ... | ... or not. |
Finding the coordinates for the points of intersection is nothing else but solving a quadratic equation. Over the real numbers this equation can have no solution. In this case the circles do not intersect. Over the complex numbers a solution always exists. So we can say that in the case of visually non-intersecting circles the intersections still exist: they have complex coordinates and we cannot see them in the real plane.
Cinderella's mathematical kernel is implemented entirely over the complex numbers. So when intersections visually vanish Cinderella does not have to deal with special cases, and it can still continue calculating - the solutions just have complex coordinates.
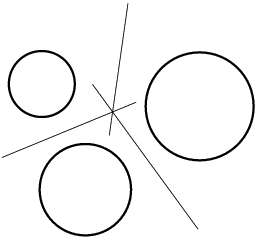
What happens if two complex points are connected by a line? In general, this line will also have complex coordinates. However, if the points are so-called complex conjugates, which means that they differ only by the sign of their complex part, then their join is again real. It is the case that the two intersections of two circles are always complex conjugates. This is the reason why the line joining them is a real line, no matter where the circles are. Cinderella will correctly calculate and draw this line, independent of the position of the circles. It may take a while to get used to the fact that intermediate results can disappear while some constructions depending on them remain visible. However, this is exactly what you should expect. Consider the case where the circles have the same radius. The line is then the perpendicular bisector of the segment joining the two midpoints. If you include the complex situations, you just have to consider less special cases.
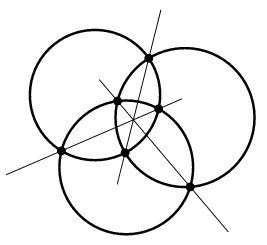
Another example for a theorem where intermediate steps disappear is the following statement about three circles. Construct the line joining the two points of intersection of each pair. The three chords that you get this way meet in a point - no matter whether the circles intersect or not.
| 
|
| Intermediate point can be complex ... | ... but theorems stay true! |
So in Cinderella each point and each line is represented by complex homogeneous coordinates. This means that altogether any point or line has a six-dimensional (!) internal representation in the mathematical kernel. This may sound crazy, but it is the most natural thing to do.
If we were satisfied with projective incidence theory then the system presented so far would be fairly complete. However, we want to be able to measure distances and angles, too. Measurements are in a sense the most fundamental geometrical operations. Unfortunately, Projective Geometry is not capable of measuring at first sight, since under perspective transformations distances can change. Actually, for a long time mathematicians considered Projective Geometry a "nice toy" for doing incidence geometry, but not appropriate for the real stuff: measuring.
History proved them wrong. With the right setup Projective Geometry is the universal system for doing measurements. This system unifies and explains different kinds of measurements, for example, it explains the relationship between Euclidean and hyperbolic geometry. However, it took a long time to finally find the algebraic setting in which Projective Geometry develops its full power. The key objects are called "Cayley-Klein Geometries" in modern terms. It is an elegant and consistent mathematical approach to measurements that combines Projective Geometry and complex numbers.
One part of this development started with the discovery of non-euclidean geometries. Our everyday geometry is, with relatively great accuracy, described by Euclid's five postulates. He used these postulates to axiomatize geometry - this happened almost 2000 years ago. The last postulate, the so-called "Parallel Axiom", plays a special role in the development of geometry. A way to formulate it is: "Whenever there is a line l in the plane and a point P not on l, then there is exactly one line through P that does not meet l."
Euclid was very cautious about using the Parallel Postulate. Large parts of Euclid's elaborations, for instance, the complete theory of congruence of triangles, were done without the explicit need for this axiom. Today we are relatively sure that Euclid himself believed that this axiom was a consequence of the other four axioms. But he could not prove this. After Euclid many other mathematicians tried to do so, some of them even presented proofs. But all these proofs were incorrect.
In the 16th to 18th century mathematicians also found many equivalent formulations for the Parallel Postulate. One of the most prominent formulations is "The inner angles in a triangle sum up to 180°." If this statement could be derived from Euclid's first four axioms then this would prove the dependence of the Parallel Postulate.
Proving that an axiom is dependent can be done by assuming its contrary and drawing conclusions until a contradiction is shown. Many people tried this, among them C.F. Gauss, J. Bolyai and N. Lobachevski. They drew conclusion after conclusion, but, to their surprise, instead of arriving at a contradiction they found themselves developing a beautiful geometric system: hyperbolic geometry. There Euclid's Parallel Postulate is modified in the following way: "Whenever there is a line l in the plane and a point P not on l, then there will be more than one line through P that does not meet l." A consequence of this assumption is that the angle sum in a triangle is always less than 180°. Between 1815 and 1824, independently from each other, these three people - who are today considered as the discoverers of hyperbolic geometry - came to the point at which they declared their system as free from contradictions, just because they could not find any. The system they developed was full of inner beauty, and it is a surprising fact that they could prove that under the assumption of the perturbed Parallel Postulate they end up with an up to trivial isomorphisms unique theory.
It is worth mentioning that most probably Gauss was the first who arrived at these conclusions, around 1816. However, he did not dare to publish his results, since he was afraid of conflicts with the leading schools of Kantian philosophy at that time. They considered a straight line as the first thing whose nature is "a priori" clear.
If you are interested in the history of mathematics we want to point you to the books of Bell [Bel1, Bel2] and Struik [Str]. As an introduction to hyperbolic geometry we recommend the book of M. J. Greenberg [Gre].
For a long time it was not clear whether the system of
hyperbolic geometry was indeed free of contradiction. What was
missing was a model of this structure, a mathematical object
that satisfied Euclid's first four axioms and the perturbed
Parallel Postulate. With minor flaws Beltrami was the first who
could construct such a model in 1868. However, the full beauty
of a general theory was first seen when Felix Klein, student of
Plücker, presented his version of what we call "Cayley-Klein
geometries", see for instance [Kl2]. What he gave was
essentially a reduction of hyperbolic geometry to constructions
of Euclidean Geometry that implies: "If Euclidean
geometry is free of contradictions then so is hyperbolic
geometry."
This finally solved all problems around
Euclid's fifth postulate.
The idea behind Cayley-Klein geometries is to use the Projective plane, and to distinguish a special conic - the "fundamental object." A special kind of global measurement is defined that depends only on the fundamental object. Depending on the type of the fundamental object you have chosen you get different types of geometries: Euclidean geometry, hyperbolic geometry, elliptic geometry, relativistic geometry, and three other geometries of minor importance.
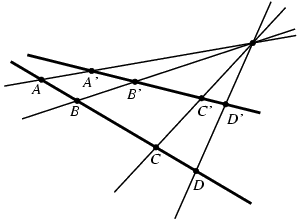
We will not go into the details of Cayley-Klein geometries, but we will present the major definitions and demonstrate some basic effects. We first need the concept of a cross ratio: For four points A, B, C and D on a line, the cross ratio is defined as the number
| (A,B | C,D) := ((A-C)(B-D)) / ((A-D)(B-C)) |
|
| The cross ratio |
The cross ratio is of remarkable value in Projective Geometry, since it is invariant under perspective transformations. So, if you have four points A, B, C and D on a line and centrally project them to four points A', B', C' and D' on another line, then the cross ratios of the two quadruples of points are identical.
Similarly, the cross ratio of four lines through a point P can be defined to be the cross ratio of four points that are the intersections of each line with another, distinct line not going throught the point P.
Now the definition of a Cayley-Klein geometry is easy. Pick a quadratic form
| ax² + by² + cz² + dxy + exz + fyz = 0. |
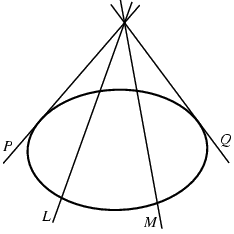
The zero set of this equation describes a, possibly complex, conic in the projective plane. This is the "fundamental object" of the geometry. Now measurements of angles and distances are defined as follows: For the distance between two points A and B take the line joining them. The intersection of this line with the fundamental object are two points X and Y. Calculate the cross ratio (A,B | X,Y). Take the logarithm of that number and call the result "distance."
Angles are calculated in an analogous way. For the angle between two lines L and M first take their meet, that is their point of intersection. The tangents through the meet that touch the fundamental object are two lines P and Q. Calculate the cross ratio (L,M | P,Q). Take the logarithm of that number and call the result "angle." Usually, these two functions are multiplied with some cosmetic constants r and s in order to match the traditional definitions of measurements.
| 
|
| dist(AB) = r·ln(A,B | X,Y) | angle(LM) = s·ln(L,M | P,Q) |
It may sound like magic, but this is all you have to know. Depending on the type of fundamental object that you have chosen you get different kinds of geometry. Up to isomorphism there are exactly seven different types of geometries you obtain that way. The three most important choices for the fundamental conic are:
Two things are worth mentioning:
The metric part of Cinderella is based on Cayley-Klein geometries. All calculations of lengths, angles, orthogonality, circles, etc. refer to a fundamental object.
We finally want show at least one effect that is caused by this general theory. We do this in order to give you a feeling for what complex numbers, cross ratios and Projective Geometry have to do with measuring.
We consider the case of Euclidean Geometry. There the fundamental object has the equation x² + y² = 0. Using complex numbers this quadratic form can be factored into two linear forms: x² + y² = (1·x + i·y + 0·z)·(1·x - i·y + 0·z). The points I := (1,i,0) and J := (1,-i,0) that occur in this formula play a special role in Euclidean Geometry. They are not affected by any euclidean transformation. In a very well defined way we can say that: "Euclidean Geometry is Projective Geometry together with I and J."
The points I and J are sometimes called the imaginary circle points, since they have a very special relation to circles: each Euclidean circle passes through I and J. To see this consider a general circle equation in homogeneous coordinates
| x² + y² + cz² + exz + fyz = 0. |
Now plug in the coordinates of I and J. Using the rules for calculating with complex numbers we observe that the circle equation is obviously satisfied. Thus we can say that a circle is a special conic that passes through I and J. With the notion of a circle it is easy to define what it means to have equal distances or equal angles. The remaining concepts of Euclidean Geometry can be derived in a straightforward manner.
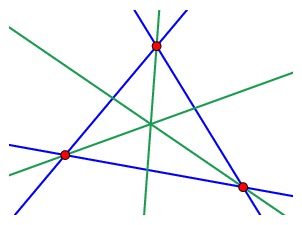
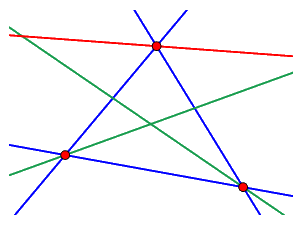
It was mentioned in the preface of this manual that Cinderella uses some basic new methods to avoid inconsistent behavior. The geometric system we presented in the previous sections is a closed framework for doing geometry, including measurements. However, so far there is a element missing that is crucial for Cinderella: dynamics. Most other systems for dynamic geometry, or parametric CAD, suffer from inconsistencies that come from an unsatisfactory treatment of the special effects of dynamics. For instance, consider the "theorem" that the angular bisectors of the sides of a triangle meet in a point. Every pair of lines has two angular bisectors which are perpendicular to each other. Depending on the choice of the angular bisectors the above statement can be true or false. Now imagine you have constructed an instance of this "theorem" (i.e. you have chosen the correct bisectors). You start to drag the vertices around and suddenly, without reason, one angular bisector flips to the other position and the "theorem" becomes false. Such a scenario can happen in a any system that does not take extra efforts to resolve the special problems from the dynamic aspects of geometry.
| 
|
| The angular bisectors of a triangle can intersect ... | ... or not |
Let us consider another small construction. Take two circles and one of their intersections. While you drag elements around Cinderella has to decide for every mouse move which intersection "you mean."
It is a good first attempt to "trace" this point of intersection using the rule: "always take the intersection that is closest to the previous position", since this precisely reflects the definition of continuity. But how should we deal with vanishing intersections? Again it pays off having implemented everything in complex space. In Cinderella intersections never vanish, they can become complex, though. So we have to trace the intersections in complex space and use the above rule.
However, this is not enough. When you separate two circles that were previously intersecting there is always a position in which the two points of intersection coincide. How can the points be distinguished in this situation? This time it is analytic function theory that rescues us. If "detours" through complex space are allowed, then there is always a path that avoids all degenerate situations. Again the whole approach is only possible since everything is embedded in a complex space.
Here is an approximate description of what happens while you drag the mouse from one position to another in the "Move" mode of Cinderella. While you move a point from position A to position B:
For the tracing Cinderella uses an adaptive step width algorithm. You can imagine that while you drag the construction elements the mouse pointer leaves the "real screen" and walks through complex space.
Why all this effort? With these methods we can be sure that elements do not "jump around" without any reason. So when you start with a correct drawing of the angular bisectors theorem you will never be able to move it to a false position. The theory forms also the basis for the reliable randomized theorem checking and for the loci and animation functions of Cinderella.