Measurements

Measuring is an important part, perhaps even the origin, of geometry. Cinderella has modes for measuring distances, angles and area. Their behavior, at least in Euclidean Geometry, is relatively straight forward:

For most purposes that is all you have to know. However, as usual, there are a lot of fine details that sometime make things harder. If you deal with non-euclidean geometries their crucial defining property is a strange way to measure things. What goes on exactly is described in more detail in the Behind the scenes section. For now it is sufficient to know that in non-euclidean geometries measurements differ from the usual Euclidean measurements. Values of distances or angles may even become complex numbers. These values can be calculated with the theory of Cayley-Klein-Geometries. The treatment of measurements in such a general way is one of the core features of Cinderella. You should not worry about the strange behavior of measurement in non-euclidean geometries. Perhaps the best way to understand it is to play with different constructions to get a feeling for the unique aspects. Allowing people to get an intuitive feel for non-euclidean geometries is one of the main goals of Cinderella.

Another fine point comes from the measurements of areas. Cinderella is able to measure the area of polygons and of conics. In both cases there are a few things that deserve some extra attention. It is easy to define the area for a polygon, that does not overlap itself. But what happens if it does? The approach chosen in Cinderella is to use a general and consistent formula for area. Areas are counted with respect to an orientation. How much a point inside the polygon contributes to the area depends on its winding number with respect to the boundary.

The area of conics is also a delicate topic. It is easy to define the area of an ellipse. But what is the area of a hyperbola? Is it infinite? Is it undefined? Is it something completely different? Cinderella chooses an algebraic approach that tries to use only one formula for all different cases. It turns out, that the area of a hyperbola is most reasonably described by a complex number. So, if you make measurements of areas of conics do not be surprised if complex numbers sometimes show up.

Remark

The measurements are shown as texts. They can be used as "text objects", so they can be dragged around and be repositioned. Consult the description of the add text mode for these features.

Distance

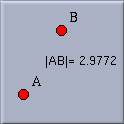
Measuring distance in Cinderella is very much like drawing a line in the "Add a line" mode. You have to select the two points whose distance from each other you want to measure. This is done with a single mouse press-drag-release sequence.

• Move the mouse pointer over the first point and press it.
• You drag the mouse, with the left button pressed, to the second point. While you drag, a ruler with the actual distance from the first point to the mouse-pointer is shown.
• The ruler snaps to selected points. If the second point is selected, you can release the mouse button.

Mouse press: a point is selected.	Mouse drag: a ruler is shown.	Mouse drag: second point selected.	Mouse Released: Measurement added.

Synopsis

Measure the distance between two points with a press-drag-release sequence.

Caution

The definition of distance changes with the type of geometry (Euclidean, hyperbolic, or elliptic). In hyperbolic geometry distances may even be complex numbers.

Angle

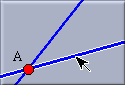
This mode is used to measure the angle between two lines. The application of this mode requires a little care. Between two lines there is not only one angle - there are two, an angle and its counter-angle. To take this fact into account, the "Angle" mode is provided with a position sensitive selection mechanism. To measure the angle, two lines have to be selected. In order to know which angle will be chosen three points are relevant: the click point of the first selection, the click point of the second selection, and the intersection of the two selected lines. Imagine a triangle formed by these three points. The inner angle at the intersection point of the lines will be measured. This is what you would intuitively expect.

Cinderella simplifies the selection process with graphical hints which show the angle that will be measured.

First selection: a line is highlighted. The selection point is memorized.	Moving the mouse: hints are shown that indicate the angle that will be measured.	Second selection: The angle is measured.

Synopsis

Measure the angle between two lines.

Caution

The definition of angle depends on the type of geometry (Euclidean, hyperbolic, or elliptic). In hyperbolic geometry angles may even be complex numbers.

Area

In this mode you can measure areas of polygons and of conics. To measure the area of a polygon you simply click inside the polygon. To measure the area of a conic, you simply select it. In particular, you can use this mode to measure the area of a circle.

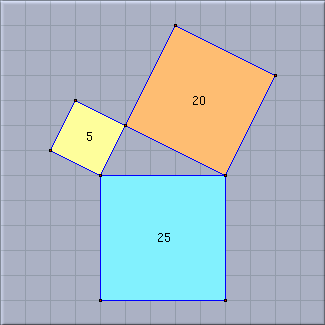Pythagoras' Theorem with area measurements

Synopsis

Select a polygon or a conic and get its area.

Caution

Areas of hyperbola are complex numbers.

The contribution of a point to the area of a polygon is calculated with respect to its "winding" number. In particular areas may become negative if the polygon is oriented clockwise. If the polygon is self-overlapping areas may be zero.