Definition modes

Definition Modes

The definition modes use a simple "define by selection" mechanism to construct new elements. You choose a certain definition mode by clicking on its icon in the tool bar, then you are asked to select a certain number of elements in the view. After enough elements are selected the newly defined element is added to the construction. Although these modes are slightly inconvenient compared to the interactive modes, it is sometimes unavoidable to use these modes. There are four major circumstances when the definition modes should be used:

A certain geometric operation is only provided as a definition mode. (This is the case for "Angular bisector", "Compass", "Circle by three points", "Center", " "Conic by five points", "Polar of a point", "Polar of a line", and "Polygon".
A point of intersection could not be reachable in the visible area of a view. For instance, two lines can be almost parallel, so that their point of intersection lies far outside the viewing region in the window. Then the usual "Add a point" or "Add a line" modes are not applicable. But you can still select the lines and apply the "Meet" mode.
An element could be invisible or complex. It can still be selected (e.g., in a "Construction Text" view) and a definition mode can be used.
A situation could be ambiguous, for instance three lines passing through a point. Then the interactive "Add point" mode cannot be used to add a point of intersection (since in these cases all three lines would be close to the mouse pointer position). In this case use the "Meet" mode and select the lines whose intersection is desired.
In the case of a geometric theorem where three lines always meet, such as the altitudes of a triangle, Cinderella's theorem checking mechanism ensures that the added point is considered incident to all three lines.

A few things are common to all definition modes and should be known in advance.

Elements are selected by clicking them with the mouse pointer. The selection can be made in any of the geometric views, in particular in the "Text view" where all elements are always visible and selectable).
Selected elements are highlighted in the view.
Preselected elements are often considered when a definition mode is chosen. So if two lines are selected and you press the button that chooses the "Meet" mode then the point of intersection is instantly added.
If you made a mistake in selecting an element you can deselect it with a second click.
You can also select the elements by moving the mouse while holding the mouse button down. All elements that are touched by the mouse pointer will be selected (resp. deselected).
Selected elements that do not contribute to the required selection of the mode are ignored. For instance, if you choose the "Circle by three points" mode, all selected lines, circles and conics are ignored.
Selection modes communicate with the user by using the message line. There you can find messages that tell you about the next expected input.

Center

This mode constructs the center of a conic. In particular you can use this mode to construct the center of a circle. For general conics the center is the intersection of its axes of symmetry. The center of a conic is sometimes useful for constructing a point on a movable conic.


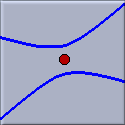Center of an ellipse	Center of an hyperbola

Synopsis

Select a conic and construct its center.

Caution

This mode is not properly supported in non-euclidean geometries, it always constructs the euclidean center.

Angular Bisector

This mode is used to construct the angular bisector of two lines. The application of this mode requires a little care, since two lines do not have only one angular bisector - they have two! To take this fact into account, this mode is provided with a position sensitive selection mechanism.

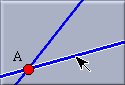
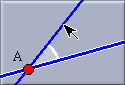
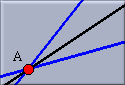
To define the angular bisector, two lines have to be selected. In order to indicate which angular bisector should be chosen three points are relevant: the click point of the first selection, the click point of the second selection, and the intersection of the two selected lines. Imagine a triangle formed by these three points. The inner angle at the intersection point of the lines will be bisected. This is what you would intuitively expect.

To make the selection process a bit simpler Cinderella gives graphical hints, as to which angle will be bisected.


First selection: A line is highlighted. The selection point is memorized	Moving the mouse: An indication of the chosen angle is given.	Second Selection: The angular bisector is added.

Synopsis

Select two lines and construct their angular bisector.

Caution

The definition of angular bisector depends on the type of geometry (Euclidean, hyperbolic or elliptic). In hyperbolic geometry angular bisectors can even have complex coordinates.

Compass

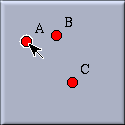
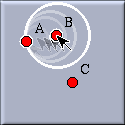
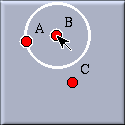
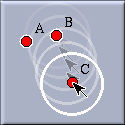
The compass is a very useful tool for transferring the distance between two points to some other place. Cinderella's compass works exactly like a real compass. You select a first point by clicking (i.e. you poke the needle into the first point). You select the second point by clicking (i.e. you adjust the compass to the distance between the first and the second point). Then you are ready to transfer the distance to another place. When you click at a third point a circle with the specified distance around this point is added to the construction.


First selection: the first point is highlighted.	Moving the mouse: hints are shown for the distance.	Second selection: the distance is fixed.	Moving the mouse: hints are shown for the position.	Third selection: the construction is finished.

Synopsis

First select two points whose distance is the radius of a new circle centered at a third point.

Caution

The definition of a circle changes with the type of geometry (Euclidean, hyperbolic or elliptic).

Mirror

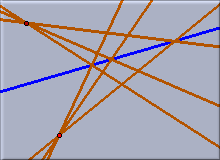
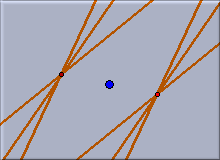
The mirror is a multi-purpose tool for doing reflections at points, lines or circles. The first mouse-click selects the "mirror". The following clicks select the elements that should be reflected. Reflected elements are either points, lines, or conics. You can deselect the mirror by clicking on it a second time. Depending on the choice of the mirror different actions are performed.

If the mirror is a line then the usual reflection is taken. The mirror image of a point with respect to a line is a point that has the same distance to the line as the original point and lies on the perpendicular of the line that goes through the original point.
If the mirror is a point then the reflection "at this point" is taken. The mirror image of a point with respect to a point is a point that has the same distance to the mirror-point as the original point and lies on the join of the mirror-point and the original point.
If the mirror is a Euclidean circle then the inversion at that circle is taken. The inverse of a point with respect to a circle is a point that lies on the join of the original point and the center of the circle. The distance of the inverse point to the center of the circle is such that the product of this distance and the distance of the center to the original point is the circle's radius squared.

Reflections of lines or conics are considered as pointwise reflections.


Reflection at a line	Reflection at a point	Inversion at a circle

Synopsis

First select a mirror. Then select elements that should be reflected.

Caution

The definition a mirror image heavily depends the choice of the underlying geometry.

Circle by Three Points

This mode is for constructing a circle that passes through three points. In Euclidean Geometry such a circle is always uniquely defined to be the circumcircle of the triangle defined by the three points. You choose the points one after another. The definition phase does not supply graphical hints.

Synopsis

Select three points. Then their circumcircle is constructed.

Caution

This mode is only available in Euclidean Geometry. In other geometries (hyperbolic, elliptic) there is no unique circle with this property.

Conic by Five Points

This mode constructs the unique conic that passes through five points. It is the basic mode for constructing a general conic.

Synopsis

Select five points to create a conic.

Caution

If four of the five points are collinear the conic is no longer unique and a null-element is computed.

Polar of a Point

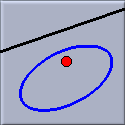
This mode constructs the polar of a point with respect to a conic. The point and the conic can be selected in any order. The polar, which is a line, is then constructed.

This mode has a few very interesting special cases that deserve some extra attention. If the point is on the conic itself then the unique tangent to the conic that passes through that point is constructed. Even more special, if the conic is a circle and the point lies on the circle then the tangent to the circle that passes through the point is constructed. Although the mode gives access to general polars this special case will most probably be its main application.

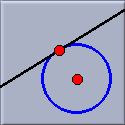General Polar Tangent to conic Tangent to circle

Synopsis

Select a point and a conic and construct the polar line of the point.

Polar of a Line

This mode constructs the polar of a line with respect to a point. The line and the conic can be selected in any order. This mode can be used to construct the point where a tangent line touches the conic.

Synopsis

Select a line and a conic to create the polar point of the line.

Polygon

In this mode a polygon can be constructed from a sequence of vertices. Select the vertices in the order in which they should appear on the boundary of the polygon. Unlike the other definition modes, this mode does not expect a fixed number of input selections. You finish the creation of a polygon by selecting the first point of it a second time to close the polygon. For instance, if you want to construct a polygon through vertices A, B, C and D, you have to select A, B, C, D and A in this order.

If you made a mistake by selecting a wrong point, you just click the point again to delete it from the boundary of the polygon. However, only the last point in the sequence can be deselected in this way.

Graphical hints guide you through the definition phase. They always resemble the part of the polygon that has been constructed so far.

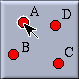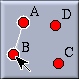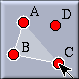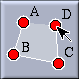1st click 2nd click 3rd click 4th click 5th click Finished

Synopsis

Select a sequence of points to define a polygon. To finish the definition select the first point again.

Caution

This mode is only supported in the Euclidean, spherical and textual view. The hyperbolic view ignores polygonal objects.

The orientation of the polygon is important when measuring its area.

Join

In this mode the line joining two points can be created. Select two points and the line connecting them is constructed.

This mode may at first sight seem to be unnecessary. You usually add lines with the interactive "Add a line" mode. However, under certain circumstances it can be unavoidable to use the join mode. For instance, even if a point is not reachable (or even complex) in a usual view, it is still listed in the "Construction Text" view where it can be selected and used for the join mode.

Synopsis

Select two points and construct their join.

Meet

In this mode the point of intersection of two line is constructed by selecting the lines.

This mode may at first sight seem to be unnecessary. Usually points are added using the "Add point" mode, or as a byproduct of some other interactive mode. However, under certain circumstances it can be unavoidable to use the "Meet" mode. For instance when the intersection of two lines is not reachable in a usual view, the lines are still listed in the "text view" where they can be selected and used for the "meet" mode. Another case where the meet mode is a good choice is in the case of ambiguities when three lines pass through one point. Then the meet mode is a secure way of adding a certain point of intersection.

Synopsis

Select two lines and create their intersection.

Define a Parallel

This mode constructs the parallel of a line through a point. Select the point and the line in arbitrary order. In many cases you can use the more comfortable interactive "Add a parallel" mode.

Synopsis

Select a line and a point and construct the parallel to the line through the point.

Caution

The behavior of this mode is very dependent on the current geometry. Whereas in Euclidean Geometry there is always exactly one parallel, in non-euclidean geometries the number of parallels depends on the definition of parallelity. Cinderella takes the algebraic point of view: A parallel to a line L is a line that has a zero angle with L. Therefore the above mode produces exactly two parallels in hyperbolic geometry.

In elliptic geometry, under the usual definition, there are no parallels at all. However, from an algebraic standpoint there exist such parallels; they just have complex coordinates. In other words, they will never be visible. Cinderella constructs these parallels. They are invisible but still present in the "Text view", where they can be used for further constructions.

Define a Perpendicular

This mode constructs the perpendicular of a line through a point. Select the point and the line in any order. In most cases you can use the more comfortable interactive "Add a perpendicular" mode.

Synopsis

Select a line and a point and construct the perpendicular to the line through the point.

Caution

The definition of perpendicularity depends on the chosen geometry.


1st click	2nd click	3rd click	4th click	5th click	Finished